Generating lexicographic permutations with parity

Lexicographically ordered permutations

Referring to wikipedia:

The following algorithm generates the next permutation lexicographically after a given permutation. It changes the given permutation in-place.

1. Find the largest index k such that a[k] < a[k + 1]. If no such index exists, the permutation is the last permutation.
2. Find the largest index l greater than k such that a[k] < a[l].
3. Swap the value of a[k] with that of a[l].
4. Reverse the sequence from a[k + 1] up to and including the final element a[n].

Sometimes, for example when evaluating an $N\times N$ determinant, we need to know whether the given sequence requires an even or an odd number of element transpositions to reach the next permutation.

Speaking of even and odd transpositions, $[a,b,c]\to [c,a,b]$ requires minimum two swaps between elements: first $b$ and $c$ are swapped to arrive at $[a,c,b]$, followed by another swap between $a$ and $c$. Thus even transpositions are required in total. Similarly, $[a,b,c]\to [c,b,a]$ requires minimum three transpositions: to the previous result, an extra swap between $a$ and $b$ is needed, resulting into an odd number of transpositions.

Some visual proofs related to transpositions

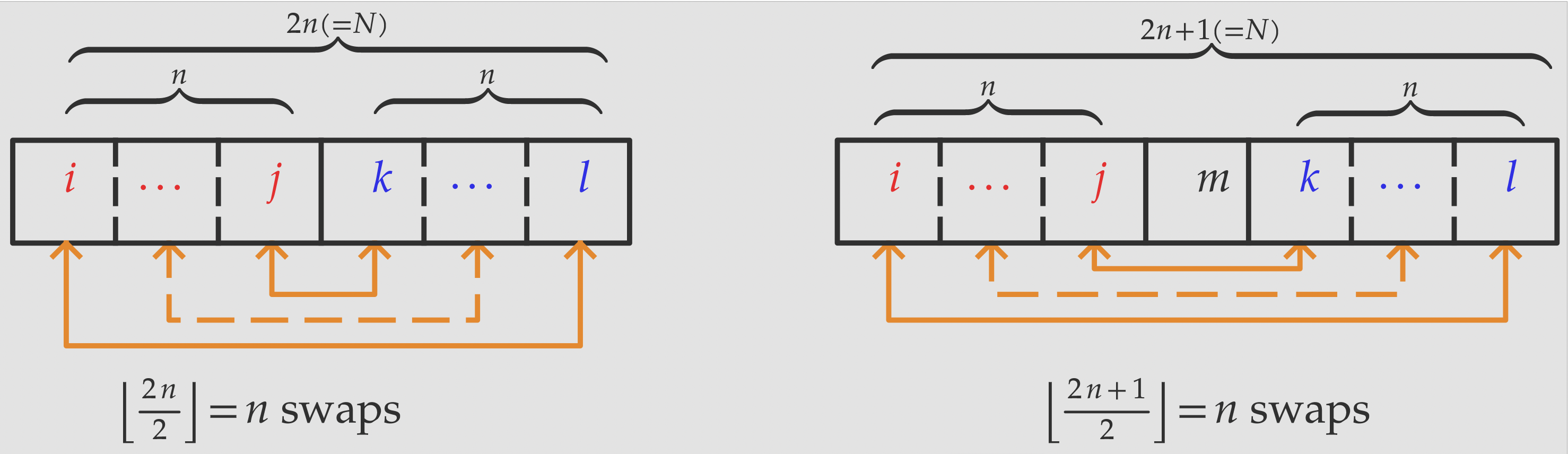
1. The number of transpositions required to swap two distinct elements in a given sequence is an odd number.

   

2. The number of transpositions required to reverse a sequence of length $N$ is $\lfloor \frac{N}{2}\rfloor$.

   

Representing parity

The parity of integers is the masure of them being even or odd. The even integers have the even parity and the odd integers have the odd parity. Thus, to represent the even parity any even integer can be used. Similarly, to represent the odd parity any odd integer can be used. To implement this algorithm we will use the integer $0$ to represent the even parity and $1$ to represent the odd parity.

Parity of the next permutation

With the proofs above we can trivially add a step to the algorithm from Wikipedia to find the parity of the next permutation:

5. Parity of the new permutation is the same as that of $$\lfloor \frac{n-k}{2}\rfloor +1$$

Note that in the referenced algorithm, the number of elements is $n$ and the index of the last element is also $n$ as evident from the fourth step. This implies the indexing used is $1$-based. If there are $n$ elements and the indexing is $0$-based, then the $n$ in the parity computation formula needs to be replaced by $n-1$ to reflect on the fact that $n$ in the above formula represents the index of the last element of the sequence.

The reasoning behind the formula is as follows: if we reach step 2 of the algorithm then at least a single swap between two distinct elements is guranteed that contributes an odd parity (1) as per the first proof above. In the step 4, we reverse a sequence of length $n-k$, which contributes $\lfloor \frac{n-k}{2}\rfloor$ as per the second proof.

Implementation in C++

The standard C++ library header <algorithm> defines the function std::next_permutation. Among the many function signatures in the header, we will keep it simple by focusing on the following declaration:

template< class BidirIt >
          bool next_permutation( BidirIt first, BidirIt last );

Although it may not be obvious from the function signature the description of the function says that the range [first, last) will be permuted, or in other words, the input range will be modified by this function. Also, notice that the return value is a boolean to indicate whether the generated permutation is lexicographically greater than the previous permutation. If it returns false, the last permutation is reached and the range will be reset to the first permutation.

Now we write a new function named next_permutation_parity that has the following signature:

template< class BidirIt >
          bool next_permutation_parity(int& parity,
                                BidirIt first,
                                BidirIt last );

The parameter parity is a reference to an integer to which the parity indicator ($0$ for even and $1$ for odd) will be written. The value in parity before the function call is the initial parity indicator of the range [first, last). Unless the initial sequence is an odd permutation of the lexicographically first sequence, the initial value of parity should be an even number.

template< class BidirIt >
          bool next_permutation_parity(int& parity,
                                BidirIt first,
                                BidirIt last ) {
  using std::iter_swap;
  using std::reverse;
  using std::distance;

  BidirIt i = last;
  if (first == last || first == --i) return false;

  for (;;) {
    BidirIt ii = i;
    --i;
    if (*i < *ii) {
      BidirIt j = last;

      while (!(*i < *(--j))) {
        // do nothing here
      }

      iter_swap(i, j);
      reverse(ii, last);

      int p = parity + 1 /* for the single iter_swap */
                     + distance(ii, last) / 2;
      parity = p % 2;

      return true;
    }
    if (i == first) {
      reverse(first, last);

      int p = parity + distance(first, last) / 2;
      parity = p % 2;

      return false;
    }
  }
}

Demo

//
// ~~~~~~~~
//
auto str = std::string{"abcd"};
int p = 0;
do {
   std::cout << p << " " << str << "\n";
} while (next_permutation_parity(p, str.begin(), str.end()));
//
// ~~~~~~~~
//

Output:

0 abcd
1 abdc
1 acbd
0 acdb
0 adbc
1 adcb
...
0 dcba